插入排序在简单排序的算法中可以说是最好的一种算法了，虽然插入排序仍然需要O(N*N)的时间，但是在一般情况下，它要比冒泡排序快一倍，比选择排序还要快一点。尽管它比冒泡排序和选择排序要麻烦一些，但是它并不复杂，它经常被用在比较复杂的排序算法的最后阶段，例如选择排序。

用插入排序为棒球队员进行排序：

    开始插入排序之前，先把棒球队员按随机顺序排成一排，从排序过程的中间开始，可以更好的理解插入排序，这时队列已经排好了一半。   

局部有序

    此时，在队伍的中间有一个作为标记的队员，将一件红色运动衫放到被标记队员的前面，在这个作为标记队员的左边的所有队员都已经是局部有序的了。这意味着这一部分人之间是按照顺序排列好的，每个人都比他左边的人高。然而这些队员在队伍中的最终位置还不确定，因为当没有拍过序的队员要插入到他们中间的时候，他们的位置还要发生变动。

    注意，局部有序在冒泡排序和选择排序中是不会出现的，这两个算法中，一组数据项在某个时刻是完全有序的，在插入排序中，一组数据仅仅是局部有序的。

被标记的队员

    作为标记的队员，被称为‘被标记’的队员，他和右边所有的队员都是无序的，如下图所示：

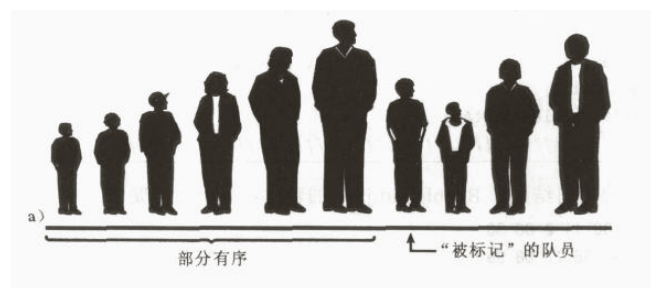
    下面将要做的是在局部有序组中的适当位置插入被标记的队员，然而要做到这一点，需要把部分已排序的队员向右腾出空间，为了提供移动所需的空间，就先让标记的队员出列，（在程序中，这个数据项被存储在一个临时变量中），如下图所示：

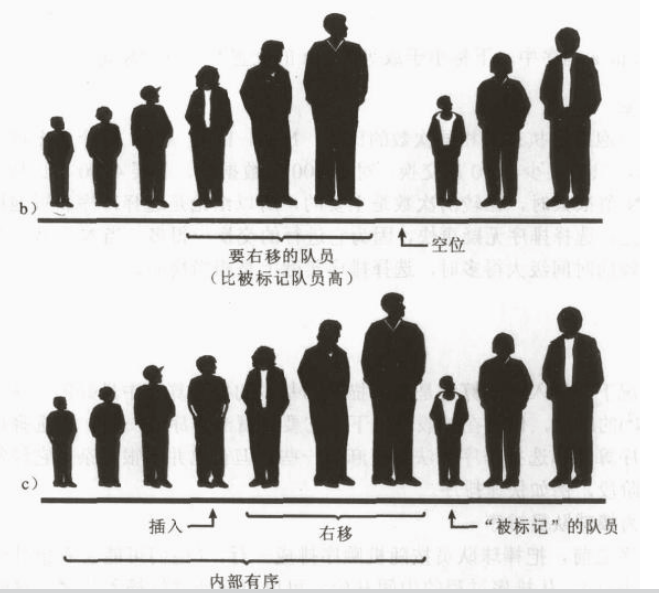
    现在移动已经拍过序的队员来腾出空间，将局部有序中最高的队员移动到原来原来被标记的队员的位置，以此类推。

    这个移动过程什么时候结束呢？假设你和被标记的队员一起向队列的左端移动，在每个位置上，队员都向右移动一位，同时被标记的队员和下一个要移动的队员进行比较，当把最后一个比标记队员还高的队员移动之后，这个移动的过程就停止了，最后一次移出空出的位置，就是被标记队员应该插入的位置。

    现在局部有序的队伍中多了一个队员，无序的队伍中少了一个队员。作为标记的运动衫向右移动一个位置，所以它仍然放到未排序的部分队员的最左边，重复这个过程，知道所有未排序的队员都被插入到局部有序的队员中。

插入排序的代码实现：

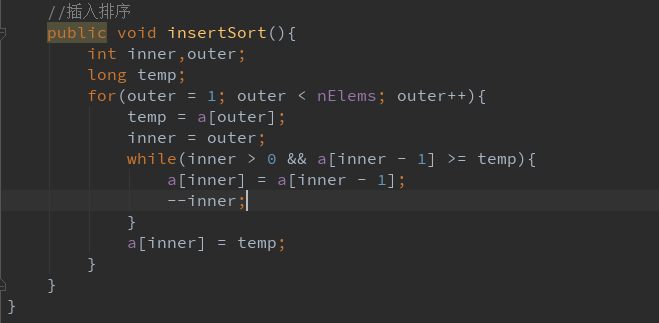
运行结果:

活动图：

插入排序的不变性：

    在每趟结束时，在将temp位置的项插入后，比outer变量下标号小的数据项都是局部有序的。

    插入排序的效率：

    这个算法需要多少次比较和复制呢？在第一趟排序中，它最多比较一次，在第二趟最多比较两次，以此类推，最后一趟 最多，比较N-1次，因此有：1 +2 +3+4+5+...+N-1 = N*(N-1)/2

    然而，因为在每一趟排序发现插入点之前，平均只有全体数据项的一半真的进行了比较，我们除以2得到 N*(N-1)/4

    复制的次数大致等于比较的次数，然而，一次复制与一次交换的时间耗费不同，所以相对于随机数据，这个算法比冒泡排序快一倍，比选择排序快一点。

    在任意情况下，对于大部分算法，对于随机顺序的数据进行排序都需要O(N*N)的时间级。

    对于已经有序或者基本有序的数据来说，插入排序要好的多，当数据有序的时候，while循环的条件总是假，所以他变成了外层循环中的一个简单语句，执行N-1次。在这种情况下，算法运行只需要O(N)的时间级。如果数据基本有序，插入排序几乎之下O(N)的时间，这对把一个基本有序的文件进行排序是一个简单而有序的方法。

    然而，对于逆序排序的数据，每次比较和移动都会执行，所以插入排序不比冒泡排序快。